Pablo Trefftz-Posada, Ph.D.

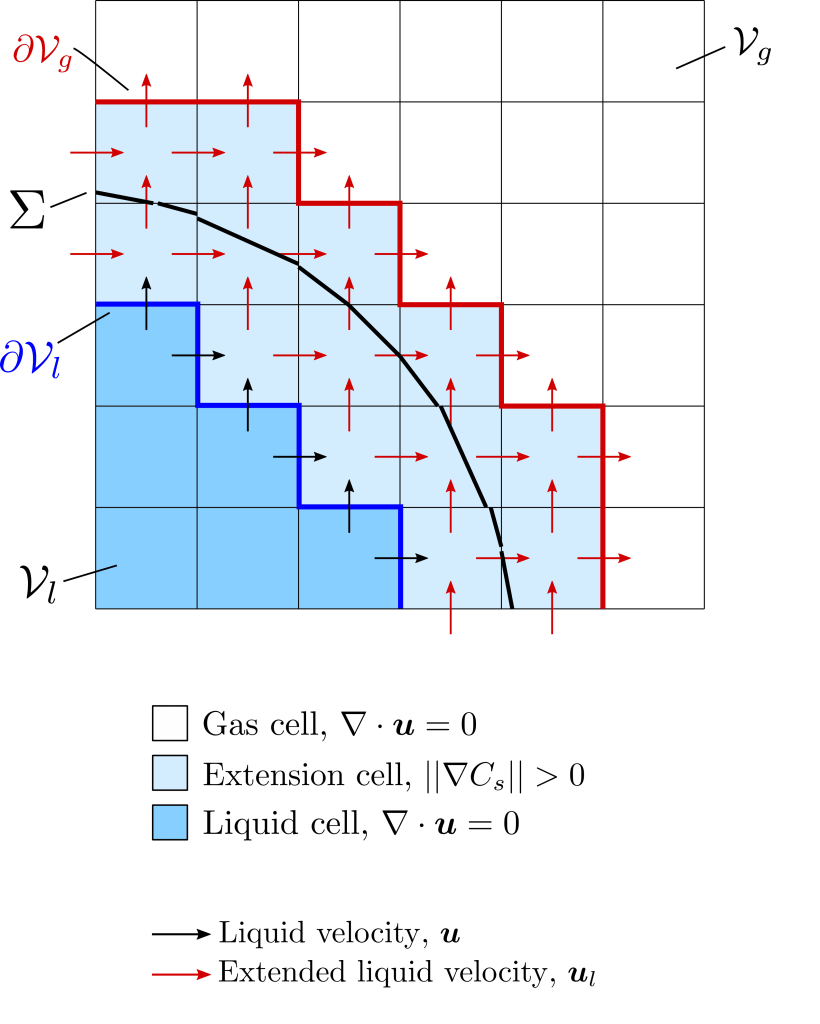
A new method is developed for simulating incompressible gas-liquid flows with phase change. The gas-liquid interface is captured using a volume-of-fluid (VoF) method that is mass conserving in the presence of evaporation and condensation. The method relies on a divergence-free extrapolation of the gas- and liquid-phase velocity fields. This allows for any VoF algorithm for incompressible flow to be used and the resulting numerical solution automatically inherits the boundedness and conservation properties of the chosen VoF scheme. The approach also has the advantage of not requiring the solution of an additional Poisson or Helmholtz equation that is often encountered in existing methods.

The interaction of dispersed droplets and turbulence is important in many natural and industrial processes, e.g., rain formation, liquid-liquid emulsion, spray cooling and spray atomization in combustors. Previous studies explained the interaction of droplets and decaying isotropic turbulence. In decaying isotropic turbulence, the absence of mean shear translates to the absence of production of TKE. Thus, the next step of complexity in our understanding of droplet/turbulence interaction, including the effects of shear on droplets and the effects of droplets on the production of TKE, is studying droplet-laden HST. The main objective of this work is to explain the physical mechanisms occurring in droplet-laden homogeneous shear turbulence (HST) with a focus on the modulation of turbulence kinetic energy (TKE) caused by the droplets. To achieve such objective, first, we performed direct numerical simulations (DNS) of HST laden with droplets of initial diameter approximately equal to twice the Taylor length scale of turbulence, droplet-to-fluid density and viscosity ratios equal to ten, and 5% droplet volume fraction. We investigated the effects of shear number and Weber number on the modulation of TKE. Then, we derived the TKE equations for the two-fluid, carrier-fluid and droplet-fluid flow in HST and the relationship between the power of surface tension and the rate of change of total droplet surface area, providing the pathways of TKE for two-fluid incompressible HST.

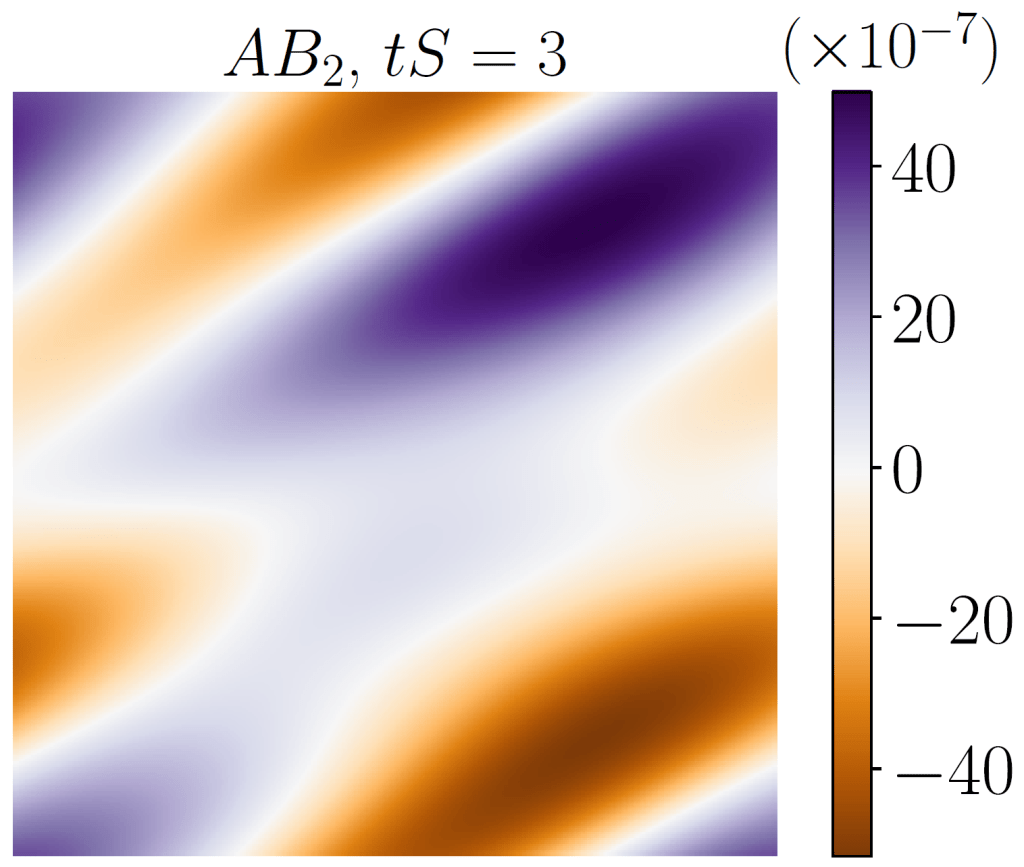
A new numerical method FastRK3P* is developed for accurately simulating immiscible two-fluid homogeneous shear turbulent (HST) flows. FastRK3P* is the result of combining the FastRK3 and FastP* methods with a newly developed mass-conserving algorithm for applying shear-periodic boundary conditions with the VoF method. Previous HST simulations used a second-order Adams-Bashforth (AB2) method which exhibits unphysical oscillations in the spectrum of turbulence kinetic energy at high wavenumbers. Crank-Nicholson and standard third-order Runge-Kutta (RK3) methods don’t exhibit these oscillations, but they require additional solutions of the Poisson equation which are computationally expensive. FastRK3P* does not exhibit these unphysical oscillations, and it requires solving the Poisson equation for pressure only once per time step instead of three times as required by the iterative Crank-Nicholson scheme or standard RK3 methodologies. The solver was verified by simulating a rotating Kelvin wave, whose structure breaks down at a shorter time for AB2 compared to FastRK3P*